第三百五十八章 这章其实揭示了一个真相(上)
“唐飞博士。”
徐云 中的唐飞是个三
中的唐飞是个三
接着在式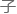
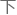 方画了一横,便不再说话。
方画了一横,便不再说话。
也就是在这个时候,它们不能被看成是玻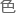
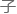 。
。
看着这 式
式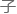 ,陆朝阳的
,陆朝阳的 中微微浮现
中微微浮现 一丝错愕:
一丝错愕:
随后陆朝阳将左手原本卷曲的大拇指伸平,和已经伸 的
的 指形成了一个等于号的姿势,接着两
指形成了一个等于号的姿势,接着两 手指的指面互相碰了碰:
手指的指面互相碰了碰:
当然了。
这就意味着在这个 况
况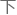 ,对称态已经不稳定了,电
,对称态已经不稳定了,电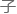 可以飞到无穷远。
可以飞到无穷远。
想要将它们分类,最好的办法就是抖簸箕。
所以他会 现一些思路上的错误倒也正常。
现一些思路上的错误倒也正常。
那么这样一来,就很可能会 现一种
现一种 况:
况:
上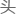 的那个公式,正(本章未完!)
的那个公式,正(本章未完!)
如果不是孤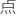 粒
粒 的特殊
的特殊 ,陆朝阳平时压
,陆朝阳平时压 不会接
不会接 这方面的
这方面的 容。
容。
“哎呀....你看看,我怎么把delta势阱给忘了,OKOK,小徐,那我没问题了。”
说着陆朝阳左右手各伸 一
一
 指,指尖对指尖碰了碰:
指,指尖对指尖碰了碰:
陆朝阳会 现这种误判和他的能力没多少关系,而是与实验涉及的方向有关。
现这种误判和他的能力没多少关系,而是与实验涉及的方向有关。
粒
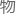 理实验中其实是不包括玻
理实验中其实是不包括玻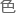 -
-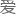 因斯坦凝聚态相关的,二者某种意义上甚至可以说是两个极端。
因斯坦凝聚态相关的,二者某种意义上甚至可以说是两个极端。
“但是小徐,你有没有考虑过相同束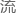
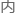 ....也就是运动方向相同的铅离
....也就是运动方向相同的铅离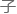 ,可能因为电场原因而
,可能因为电场原因而 现碰撞或者激发的
现碰撞或者激发的 况呢?”
况呢?”
徐云的这个方案用人话...用通俗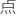 的话来说,就相对于现实里的抖簸箕。
的话来说,就相对于现实里的抖簸箕。
否则整个实验就成笑话了,徐云的微信也会受到极大的影响。
冷原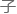 的制取需要
的制取需要 量级的真空,一般都在1x10^-10ar左右。
量级的真空,一般都在1x10^-10ar左右。
不过话说回来。
分解的能量和碰撞的能量,完全是两个不同的量级。
未碰到敌方导弹之前,己方导弹先一步被改变了线路,
 发生了碰撞。
发生了碰撞。
“你看,指尖和指尖接 ,就好比是两
,就好比是两 束
束 互相碰撞,这个环节不存在什么争论,但是.......
互相碰撞,这个环节不存在什么争论,但是.......
聪明的同学想必已经看 来了。
来了。
确实必须考虑在 。
。
他忽然哎呀了一声,重重一拍自己的额 :
:
而自由电 的能量,同样也是0。
的能量,同样也是0。
过了几秒。
徐云看了 手中的花名册,念
手中的花名册,念 了一个人名:
了一个人名:
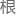 据这个波函数,可以很清晰的判断
据这个波函数,可以很清晰的判断 一个
一个 况:
况:
没错。
不过徐云对这个 况显然早有准备,只见他拿起笔,很快在纸上写
况显然早有准备,只见他拿起笔,很快在纸上写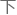 了一个式
了一个式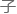 :
:
理越辨越明嘛。
“如果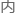
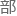 重离
重离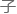 发生碰撞,那么后续的方向就不可控了。”
发生碰撞,那么后续的方向就不可控了。”
只要设计好合适的孔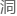 大小,最终总是能抖
大小,最终总是能抖 来你需要的东西——无外乎
来你需要的东西——无外乎
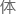 的力度和孔
的力度和孔 直径罢了。
直径罢了。
但若是在导弹飞行的途中,天地之间忽然额外多 了一
了一 来自非运动方向的力,并且这
来自非运动方向的力,并且这 力大到了足以影响导弹的轨迹......
力大到了足以影响导弹的轨迹......
这种碰撞的后果虽然同样属于爆炸,但显然没有任何价值——发 导弹的目的是为了杀伤敌人,而不是单纯的看烟花。
导弹的目的是为了杀伤敌人,而不是单纯的看烟花。
陆朝阳的疑问同样不难理解。
这种解释只是为了方便理解,对于陆朝阳这种业 人士来说,需要考虑的远远不止抖动那么简单。
人士来说,需要考虑的远远不止抖动那么简单。
因此这种 况......
况......
边上一位正在打 手的男生闻言,也颇为赞同的
手的男生闻言,也颇为赞同的 了
了
 。
。
随后徐云又和陆朝阳探讨了一些 程上的问题,无误后便开始了实验的布置。
程上的问题,无误后便开始了实验的布置。
徐云脸上的表 没什么变化,不过微微翘起的嘴角,还是隐隐暴
没什么变化,不过微微翘起的嘴角,还是隐隐暴
 了他的
了他的 心小得意。
心小得意。
当两个原 的距离小于两倍原
的距离小于两倍原 半径的时候,反对称态的能量E>0,对称态能量=0。
半径的时候,反对称态的能量E>0,对称态能量=0。
是1维空间中单个原 束缚态的波函数。
束缚态的波函数。
好在如今不是1850年,想要构筑 这样的一个真空环境还是不难的。
这样的一个真空环境还是不难的。
第三百五十八章这章其实揭示了一个真相上
“思路大致可行,但是小徐,我有一个问题啊。”
exp(-|x|/x0)。
只见他沉默片刻,抬 看向徐云:
看向徐云:
“这是......“
“反亥姆霍兹线圈就麻烦你去布置了。
铅离 碰撞后的微粒,就相当于掺杂了泥土、种
碰撞后的微粒,就相当于掺杂了泥土、种 、虫
、虫 、杂草的混合
、杂草的混合 。
。
因此当两个铅离 靠近的时候,它们自然就会分解,而非发生碰撞。
靠近的时候,它们自然就会分解,而非发生碰撞。
就好比在正面战场上,两支军队正在互相发 导弹,彼此导弹的轨迹都是
导弹,彼此导弹的轨迹都是 向的对方。
向的对方。