。在某种意义，

        必须加上某些没有任何几何解释的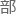件。霍奇猜想断言，对于所谓影代数簇这

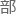        种特别完的空间类型来说，称作霍奇闭链的件实际上是称作代数闭链的几何

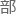        件的（有理线）组合

        「千僖难题」之三庞加莱（Poincare）猜想：如果我们伸缩围绕一个苹果表

        面的橡带，那么我们可以既不扯断它，也不让它离开表面，使它慢慢移动收缩

        为一个。另一方面，如果我们想象同样的橡带以适当的方向被伸缩在一个轮

        胎面上，那么不扯断橡带或者轮胎面，是没有办法把它收缩到一的。我们说，

        苹果表面是「单连通的」，而轮胎面不是。

        大约在一百年以前，庞加莱已经知，二维球面本质上可由单连通来刻画，

        他提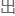三维球面（四维空间中与原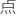有单位距离的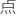的全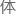）的对应问题。这个

        问题立即变得无比困难，从那时起，数学家们就在为此奋斗。

        「千僖难题」之四黎曼（Riemann）假设：有些数有不能表示为两个更小的

        数的乘积的特殊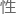质，例如，2，3，5，7，等等。这样的数称为素数；它们在纯

        数学及其应用中都起着重要作用。

        在所有自然数中，这种素数的分布并不遵循任何有规则的模式；然而，德国

        数学家黎曼（1826~1866）观察到，素数的频率紧密相关于一个心构造的所谓

        黎曼蔡塔函数z（s的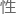态。著名的黎曼假设断言，方程z（s）=0的所有有意义

        的解都在一条直线上。这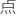已经对于开始的1，500，000，000个解验证过。证明

        它对于每一个有意义的解都成立将为围绕素数分布的许多奥秘带来光明。

        「千僖难题」之五杨－米尔斯（Yang-Mills）存在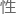和质量缺：量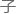

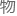
        理的定律是以经典力学的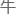顿定律对宏观世界的方式对基本粒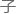世界成立的。大

        约半个世纪以前，杨振宁和米尔斯发现，量理揭示了在基本粒理与几何

        对象的数学之间的令人注目的关系。

        基于杨－米尔斯方程的预言已经在如的全世界范围的实验室中所履行的

        能实验中得到证实：布罗克哈文、斯坦福、欧洲粒理研究所和筑波。尽

        如此，他们的既描述重粒、又在数学上严格的方程没有已知的解。特别是，被

        大多数理学家所确认、并且在他们的对于「夸克」的不可见的解释中应用的

        「质量缺」假设，从来没有得到一个数学上令人满意的证实。在这一问题上的

        展需要在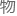理上和数学上两方面引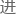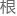本上的新观念。

        「千僖难题」

        之六纳维叶－斯托克斯（okes）方程的存在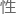与光